強化式學習筆記：從 MDP 框架到 DQN 方法

Table of Contents

背景 #

大約兩個多月前，我在強化式學習雜記一文中紀錄了一些個人感想，同時進行了在小遊戲上訓練 DQN 的 Asteroids-AI 專案。會選擇研究強化式學習的原因除了深度學習本身很有趣之外，主要希望能擴展我對機器學習整體的認識，多一種的思考問題的可能角度。

實驗告一段落之後，我原想從 DQN 文章開始回溯釐清一些疑問，後來發現還是老老實實的看一下經典課本 Sutton & Barto 的 Reinforcement Learning - An Introduction 更有助於系統性的了解領域的語言（Sutton 本人有提供全文下載）。

本文紀錄了我從 Markov Decision Process 開始，到了解 Deep Q-Network 方法為止對相關觀念的理解和筆記。

1. 框架 #

廣義來說，模型是人類對各種複雜現象本質性的理解與化簡，提供了我們得以思考、評估、量化、做出預測並用於解決問題的框架。

包含深度學習的回歸和分類器在內的監督式機器學習成果告訴我們，只要問題拆解後能夠以 $$ X \rightarrow y $$ 的輸入輸出配對方式表達，並且取得足量的有效資料，那我們就有機會用機器學習方法從資料中學習出具有一定泛化能力（Generalization）的模型或是函數近似（Function Approximation）來從輸入預測輸出。

強化式學習的課題 #

強化式學習試圖處理的問題是「代理人如何藉由與環境的互動並基於獎勵的引導來學會達到目標的方法」。

對人類的日常經驗來說，依照回饋來修正自己行爲並不陌生，強化式學習乍看之下也和監督式學習頗爲相似，然而在一連串的互動和偶爾得到獎勵的情境下，學習該如何進行？要拿什麼作為輸入？又該如何定義答案？稍微思考後便會發現這過程並不簡單，雖然同為有目標的機器學習，卻似乎無法用函數擬合的方式理解。

原因無他，強化式學習問題本身面對的是更複雜的情境，因此需要額外的模型框架來描述，而其中最重要的基礎就是為領域建立了形式化數學框架的馬可夫決策過程 Markov Decision Process（MDP）。一些奠基於此的重要概念包含

期望累積折扣獎勵（Expected Discounted Return）
狀態價值（state value）
行動價值（state-action value）
貝爾曼期望方程式（Bellman expectation equation）
貝爾曼最優方程式（Bellman optimal equation）
時序差分學習（Temporal Difference Learning）

這些觀念和 MDP 共同構成了理解強化式學習的階梯。

2. 環境與代理人 #

graph LR A[Agent] -- Action --> E[Environment] E -- Reward --> A E -- Observation --> A

在強化式學習的問題中，首先要區別「環境（Environment）」與「代理人（Agent）」並了解兩者如何互動。代理人是學習的主角，環境則是代理人所在的世界或是系統，決定了代理人能取得的外在資訊。以遊戲的情境來說代理人就是玩家或者是遊戲 AI，環境則是遊戲本身。

兩者之間的互動介面包含三種資訊 #

觀察（Observation）又稱狀態（State）
行動（Action）
獎勵（Reward）

代理人對環境的了解來自於觀察和獎勵，而環境會根據其機制以根據代理人的行動決定新的狀態並提供對應的回饋。根據不同問題的假設，代理人不一定會掌握環境的知識，在實際問題中環境的動態機制對代理人來說可能像是黑盒子，好比駕駛人會知道自己踩下油門並看到汽車加速前進，但並不會知道汽車是如何運作的。

獎勵作為目標的信號 #

當你漫無目的上路，觀察到的狀態景色會隨著你不同的行動而改變，但你選擇的路徑並沒有所謂好壞可言，因為沒有任何衡量基準在。當你的目標是「盡快回家」時，就產生了最短路線和繞遠路的差別；又若你的目標是「平安到家」，則安全駕駛就會優於搶快超車。

「獎勵」在強化式學習中扮演的指引目標的角色，環境透過提供獎勵的方式來衡量代理人的表現，進而決定學習的方向。透過獎勵代理人可以了解「要達成的是什麼」，但不是如何達成，如何達成目標的策略是代理人成功學習後的成果。

3. 馬可夫決策過程 #

以 $S$ 代表 State（或 Observation）、$A$ 代表 Action、$R$ 代表 Reward，並考慮時間步驟 $ t = 0,1,2,... $ ，我們將代理人與環境的互動用符號作形式化的描述：根據觀察到的狀態 $S_0$ 代理人採取了行動 $A_0$，接著環境給出了回饋 $R_1$ 而新的狀態變成 $S_1$，依此類推。

$$ S_0 \xrightarrow{A_0} (R_1, S_1) \xrightarrow{A_1} (R_2, S_2) \xrightarrow{A_2} ... $$

或直接看成 $S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, ... $ 這樣的序列軌跡。

這裡採取的時間標記方式將行動 $A_t$ 之後得到的報酬表達為 $R_{t+1}$ 而非 $R_t$，以強調獎勵作為行動後果的模型詮釋。

動態函數 #

在 $(S_t,R_t)\rightarrow(S_{t+1},R_{t+1}) $ 一式中的「箭號」部分代表著環境本身的機制，稱為動態函數（dynamic functions）或是轉移函數（transition functions），可用一個機率函數 $p$ 將這個過程形式化為：

$$ p(s^\prime,r|s,a) = Pr \lbrace S_t=s^\prime, R_t=r | S_{t-1}=s, A_{t-1}=a \rbrace $$

意即在給定 $s,a$ 的情況下，新狀態和獎勵組合 $s^\prime, r$ 的機率分布是確定的。注意透過 $p$ 所確定下來的是事件的機率分布而不是確定會進入某一個狀態和獎勵這樣的決定性轉換，換句話說 MDP 模型容許環境具有隨機性。

環境動態函數 $p$ 是同時考慮了狀態和獎勵組合分佈的一般性敘述，亦可以分別定義隨機狀態轉移函數 $T(s,a,s^\prime)$ 和獎勵函數 $r(s,a)$ 來代表狀態和獎勵的動態函數。

馬可夫性質 #

此一形式的成立依賴於 MDP 模型的核心假設馬可夫性質：當前的狀態包含了所有與未來相關的資訊（The future is independent of the past, given the present），因此動態函數不需要考慮任何過去的歷史狀態，僅需要給定 $s,a$ 為條件。

4. 目標與獎勵 #

代理人與環境的互動是一個持續的過程，而環境獎勵也可能多次發生，因此代理人追求的目標應該是整個過程中累積的總獎勵。若從決策的角度來看，那麼在任何一個時刻 $t$ 其過去發生的歷史也已經不重要，真正要關注的是你採取的行動如何讓未來的總獎勵最高，這個目標稱為「回報」（Return），表達為 $$ G_t = R_{t+1} + R_{t+2} + R_{t+3} + ...$$ （註：$R_{t+1}$ 代表的就是時刻 $t$ 當下採取行動 $A_t$ 後得到的獎勵，我們並沒有漏掉當下行動的獎勵）

又基於以下兩個主要考量，模型引入介於零到一之間的折扣因子 $\gamma$ 作為調節的參數

互動不一定有明確的結束（不一定是回合性 episodic 的）因此總獎勵可能會很大、無限大
相對於不確定高的遙遠未來獎勵，我們應該更重視近期的獎勵

加入折扣因子後的回報可以寫作 $$ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ...$$

或整理為常見的形式 $$ G_{t} = \sum_{k=t+1}^{T}\gamma^{k-t-1} R_{k} $$ 其中 $T$ 代表互動終止的回合（$T$ 可以是 $\infin$，只要同時 $\gamma\neq1$ 就好）。

最大化「累積折扣獎勵」也就是強化式學習代理人的目標。

5. MDP 的五元組 #

綜合目前的討論，我們可以將 MDP 用 $\langle \cal{S}, \cal{A}, \mathit{T}, r, \gamma \rangle $ 五元組更具體的表達。

$\cal{S} $ ＝狀態空間（state space，由狀態組成的集合，$S_t \in \cal{S}$）
$\cal{A} $ ＝行動空間（action space，由行動選擇組成的集合，$A_t \in \cal{A}$）
$T$ ＝隨機狀態轉移函數
$r$ ＝回饋函數
$\gamma$ ＝折扣函數（折扣因子）

以 Atari 遊戲的 DQN Agent 例子來看會比較容易理解。

代理人的觀察是遊戲畫面，$\cal{S} $ 代表了值在 0～255 之間、大小為 210＊160＊3 的陣列們所構成的集合。
以 Gymnasium 套件來說其中定義了 18 種代理人夠選擇的遊戲操作動作，$\cal{A} $ 代表這些行動構成的集合。
任何時候遊戲系統都能根據代理人的輸入計算出下一步的遊戲狀態以及分數的變化，故 $T$ 和 $r$ 為遊戲系統本身。
$\gamma$ 是 MDP 模型的參數，可以簡單地選擇一個常數例如 0.99。

在這裡輕鬆帶過的 $T$ 和 $r$ 在現實應用上可能是最大的困難，因為這可能代表著需要花費大量心力建立必要的虛擬環境來提供給代理人互動學習。畢竟在現實世界裡失敗的成本往往太高，不可能為了訓練自動駕駛而真的讓汽車上路亂開。

理解 MDP 的 $\langle \cal{S}, \cal{A}, \mathit{T}, r, \gamma \rangle$ 內容有助於將問題置於強化式學框架中思考，類似於 $X \rightarrow y$ 之於監督式學習。

6. 策略與價值函數 #

強化式學習中的代理人面對的課題是「如何選擇行動才能達到最大化回報 $G_t$ 的目標」。$G_t$ 代表了自時間 $t$ 開始往後的互動結果中將會得到的折扣後獎勵總和，不同的行動選擇會導致不同的互動過程和獎勵並影響最終回報。

這一連串的選擇反映的是代理人的行動選擇「策略」，可以用一個函數 $\pi(a|s)$ 來表達在給定狀態 $s$ 之下代理人會如何選擇行動 $a$。有時很容易忘記 $\pi$ 是機率分布函數，只要記得「隨機選擇」也是一種策略就好（例如不管在任何 $s$ 之下都各有 0.25 的機率選擇向上、下、左、右移動）。

網格世界的思考 #

想像代理人在一個能夠上下左右移動的方形地圖上尋找寶藏，其所在的位置也同時代表了狀態，為了取得最大的累積折扣獎勵代理人應該如何思考？

你也許會想，我要是能知道在當下的狀態時採取每一個行動各自能帶來的回報是多少，也就知道該選擇哪一個行動才對了，然而困難就在於我們並不知道每個行動最終回報的，所以這並沒有解決問題。雖然是這樣沒錯，但將策略問題轉化爲回報的估計的問題其實正是價值學習方法（value-based learning）的第一步。

對於一個處於狀態 $s_0$ 的代理來說，假設已知選擇向上下左右移動時分別能得到獎勵 $r_{u}$, $r_{d}$, $r_{l}$, $r_{r}$，那自然是獎勵較高者吸引人。但考慮到遊戲並非在一次互動後就結束而真正目標其實是「累積折扣獎勵」時，就需要同時考慮下一步時可以取得的回報，如此才不會為了眼前的好處而略了未來的獲利。

這也點出了很重要的遞回關係：當前的回報 $G_t$ 可以用立即獎勵 $R_{t+1}$ 和下一步起算的回報 $G_{t+1}$ 表達： $$ \begin{array}{lll} G_t &=& R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... \newline &=& R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + ...) \newline &=& R_{t+1} + \gamma G_{t+1} \end{array} $$ 也就是說，我們需要比較的是採取不同行動的條件下各自算出來的 $R_{t+1}+\gamma G_{t+1}$ 大小。

然而，目前的條件尚不足以將 $G_{t+1}$ 確定下來，這是因為回報取決於後續「每一個步驟所選取的行動而不只是單一次的選擇」，因此我們需要以「行動策略」的概念來考慮及比較回報。為此，我們定義狀態價值函數 $v_{\pi}(s)$ 來代表狀態 $s$ 在遵循策略 $\pi$ 的情況下能得到的累積折扣獎勵。

假使我們令 $\pi_{u}$ 代表總是選擇向上走的策略，$\pi_{d}$ 代表總是選擇向下走的策略，並假設從 $s_0$ 狀態開始兩種策略將分別導致進入新狀態 $s_u$ 和 $s_d$，則藉由比較 $r_{u} + \gamma v_{\pi_{u}}(s_{u}) $ 和 $r_{d} + \gamma v_{\pi_{d}}(s_{d}) $ 的大小，代理人將可以判斷哪個策略能帶來更高的回報。

狀態價值函數 #

狀態價值函數 state-value function 的正式定義為 $$ v_{\pi}(s) = \mathbb{E}_{\pi}[ G_t | S_t = s] $$

由於環境狀態的轉移函數、獎勵函數、以及策略本身都可能包含隨機性，故需要考慮取期望值 $\mathbb{E}_{\pi}$ 的概念。從隨機實驗的角度來想比較容易理解：$ v_{\pi}(s) $ 可以理解我們重複無數次實驗後得到的 $G_t$ 平均值，其中每一次都是從狀態 $s$ 開始並總是遵循策略 $\pi$ 來選擇行動。

然而，要能夠直接使用狀態價值函數作為策略其實有先決條件，其中之一是代理人需要掌握環境的動態（dynamics，包含狀態轉移函數和獎勵函數），如此才能知道從 $s_0$ 往上走後會得到獎勵 $r_u$ 並且會進入狀態 $s_u$。

行動價值函數 #

一個更直接的做法是估計「狀態加行動」的價值，我們定義行動價值函數 action-value function 為 $$ q_{\pi}(s,a) = \mathbb{E}_{\pi} [G_t | S_t = s, A_t = a ] $$

和狀態價值函數一樣，我們可以將 $ q_{\pi}(s,a )$ 想像為重複無數實驗後會得到的 $G_t$ 平均值，其中每一次實驗都是從狀態 $s$ 開始並且固定選擇行動 $a$，接下來遵循策略 $\pi$ 來選擇行動。

使用行動價值函數作為策略很容易，只要拿它算出目前狀態下每個行動各自的價值，取最高即可。

7. 貝爾曼期望方程 #

MDP 的互動序列和狀態價值適合以狀態圖來幫助理解，想像由兩種類型的節點構成的圖：狀態 $S$ 和狀態–行動 $(S,A)$。

每個實際狀態 $s$ 之下可能接續著不同的狀態–行動狀態節點 $(s,a), (s,b)...$；而每個實際狀態–行動節點 $(s,a)$ 之後則可能進入不同的新狀態 $s^\prime, s^{\prime\prime},...$。

隨著時序推演兩者層層交替串連構成樹，描繪出各種可能的演變軌跡，取得不同的最終回報。環境動態函數在描述的也就是轉移過程的機率和所得到的獎勵資訊。

下面兩張圖取自原書，視覺化的表達對於理解 MDP 和價值函數很有幫助。

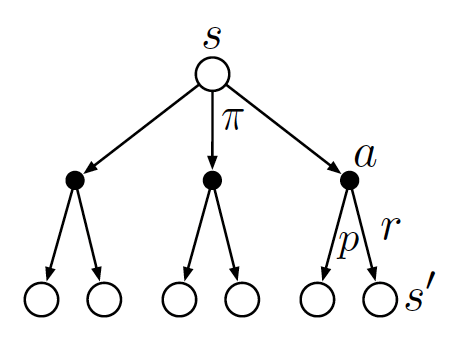
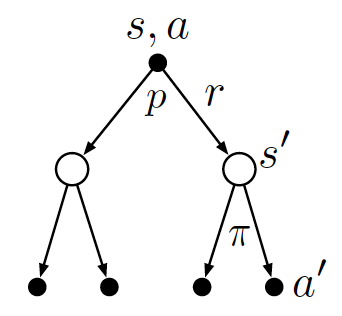
Backup diagram for state value (from Sutton & Barto)

Backup diagram for state-action value (from Sutton & Barto)

展開一層：狀態價值函數和行動價值函數的串聯 #

狀態價值 $v_\pi(s)$ 描述的是狀態 $s$ 的預期回報，而回報首先取決於你下一步的行動 $a$，這個過程可以用節點 $s$ 和其後續可能的狀態–行動節點來想像。

考慮這個特殊的情況：在策略 $\pi$ 之下代理人面對 $s$ 會固定選擇單一行動 $a$ ，則根據定義代理人預期會得到回報就是 $q_\pi(s,a)$，注意行動價值表達的已經是自此之後長期的回報，因此在這裡狀態價值 $v_\pi(s)$ 也就等於行動價值 $q_\pi(s,a)$。

更一般來說，策略 $\pi$ 決定的是行動選擇的機率分布，因此狀態價值必須綜合考量每個行動的機率和所取得的回報（一樣不需再往後考慮進入的新狀態，因為這層考慮已由接續的行動價值函數代表）： $$ v_\pi(s) = \mathbb{E}_\pi [q(S_t,A_t) | S_t = s ] = \sum_a \pi(a|s) q_{\pi}(s,a) $$

同樣的，行動價值函數 $q_\pi(s,a)$ 也可以用狀態價值函數表達，假設我們採取行動 $a$ 後得到立即獎勵 $r$ 並進入了新狀態 $s^\prime$，同樣因為 $v_\pi(s^\prime)$ 已經代表了進入狀態 $s^\prime$ 後的長期回報，因此行動價值也就可以寫作 $r+v_\pi(s^\prime)$。

一般性的表達一樣需要考慮到環境動態的隨機性，因此使用期望值的方式表達： $$ q_\pi(s,a) = \mathbb{E} [R_{t+1} + v_\pi(S_{t+1}) | S_t=s, A_t=a] = \sum_{s^\prime,r} p(s^\prime,r|s,a)[r+v_\pi(s^\prime)] $$

以上我們看見當我們以圖的方式思考、用環境動態和策略函數來描述不同互動軌跡的機率、並以期望值加來估計回報時，則 $v$ 可以用後續節點的 $q$ 展開，而 $q$ 也可以用後續節點的 $v$ 展開。

展開兩層：價值函數自身的遞迴 #

如果我們再套用一次相同的做法，則價值函數 $v_\pi(s)$ 和 $q_\pi(s,a)$ 就可以和「下一個時間步驟」的價值函數自身串連起來，其結果為貝爾曼期望方程式（Bellman Expectation Equation），其形式正如同前面我們已經看過回報 $G_t$ 的遞迴表達。

$$ \begin{array}{lll} v_{\pi}(s) & = & \mathbb{E}_{\pi}[ G_t | S_t = s] \newline & = & \mathbb{E}_{\pi}[ R_{t+1} + \gamma G_{t+1} | S_t = s] \newline & = & \sum_{a} \pi(a|s) \sum_{s^\prime,r} p(s^\prime, r | s, a)[r + \gamma \mathbb{E}_{\pi} [G_{t+1} | S_{t+1} = s^\prime]] \newline & = & \sum_{a} \pi(a|s) \sum_{s^\prime,r} p(s^\prime, r | s, a)[r + \gamma v_\pi(s^\prime)] \end{array} $$

$$ \begin{array}{lll} q_{\pi}(s,a) & = & \mathbb{E}_{\pi}[ G_t | S_t = s, A_t = a] \newline & = & \mathbb{E}_{\pi}[ R_{t+1} + \gamma G_{t+1} | S_t = s, A_t = a] \newline % & = & \sum_{r,s^\prime} p(s^\prime, r | s, a) [ r ] \newline % & & +\gamma \sum_{r,s^\prime} p(s^\prime, r | s, a) \sum_{a^\prime} \pi(a^\prime|s^\prime) % [ \mathbb{E}_{\pi}[G_{t+1}|S_{t+1}=s^\prime,A_{t+1}=a^\prime] ] \newline & = & \sum_{s^\prime,r} p(s^\prime, r | s, a) \newline & & [r + \gamma \sum_{a^\prime} \pi(a^\prime|s^\prime) \mathbb{E}_{\pi}[G_{t+1}|S_{t+1}=s^\prime,A_{t+1}=a^\prime] ] \newline & = & \sum_{s^\prime,r} p(s^\prime, r | s, a) [ r+ \gamma \sum_{a^\prime} \pi(a^\prime|s^\prime) q_{\pi}(s^\prime,a^\prime) ] \end{array} $$

類似這樣的關係式可以從資訊更新方式的角度來圖像化的思考：如何使用後續狀態的估計值來更新當下狀態的估計。Sutton & Barto 中稱這種圖為 back-up diagram。

策略評估：計算策略的狀態價值 #

在環境動態已知的情況下，貝爾曼方程式可以用於計算遵循給定策略時所對應的狀態價值函數，稱為策略評估 Policy Evaluation。

當我們使用實際問題中的 $p$ 和 $\pi$ 帶入貝爾曼方程式展開，就可以將每一個狀態的價值函數用其可能後續狀態的價值函數表達的關係式。假設問題包含 $N$（$=|\cal{S}|$）個狀態，我們會得到 $N$ 組 $N$ 個未知數的聯立方程式，方程式的解就是策略的狀態價值。

透過迭代的方式來計算價值函數的演算法稱為迭代策略評估（Iterative Policy Evaluation），其做法是將貝爾曼方程式改視為一種數值更新的規則： $$ v_{k+1} = \sum_{a} \pi(a|s) \sum_{s^\prime,r} p(s^\prime, r | s, a)[r + \gamma v_k(s^\prime)] $$ 在 $k=0,1,2,...$ 的迭代步驟中，從隨機的值出發（但注意 terminal state 要一開始就設為零），將前一輪的估計 $v_k$ 帶入等號右邊並賦值給左邊作為新一輪的估計 $v_{k+1}$，最終將會逼近 $v_\pi$。

強化式學習中的動態規劃 #

迭代策略評估方法屬於動態規劃 Dynamic Programming（DP）方法的一種。這是因為貝爾曼方程式的遞迴關係將「計算目標狀態價值的問題」拆解為「計算後續狀態狀態價值」子問題，因此具有 DP「最優子結構」（問題的最優解依賴於其子問題的最優解）和「重疊子問題」（子問題會重複出現，只需計算一次）的兩大特性。

由於我對動態規劃的理解來自傳統的資料結構與演算法，看過的問題都是最底層的子問題可以得到精確的解，並直接被用於建構更大問題的解這樣的模式。然而在強化式學習的情境中並不存在似類似的可以被精確解出的最底層問題，因此一直很困惑為何兩種都被稱為動態規劃問題。後來才知道這兩著之間的差異源自於「是否存在狀態的循環依賴」，MDP 中的動態規劃通過迭代方法解決了循環依賴的問題。

不同於傳統演算法裡的動態規劃問題，MDP 雖然將當下狀態的價值問題拆解為下一步狀態的價值問題，但狀態之間通常存在著循環依賴（非有向無環圖），因此並沒有一個底層終點可以直接取得確定性的數值。而迭代策略評估之中的「迭代」目的就是從一個初始估計一步步逼近收斂到真正的解，而這種方法的成立則奠基於「基於貝爾曼方程式的更新的規則」是一個收縮映射的過程。

關於表格型方法 #

由於我的強化式學習經驗是從訓練玩小遊戲的 DQN 模型開始，因此會自然的用 Atari 遊戲環境當作例子來思考，但這其實導致我一開始在學習某些觀念時卡關。

例如對 Atari 環境而言「使用環境動態函數來計算期望值」實際上是不可行的，因為我們並沒有關境動態函數，而我也無法想像該如合取得或準備這項資訊。又例如「迭代策略評估方法」中替所有可能的狀態 $|\cal{S}|$ 計算其價值函數對 Atari 環境來說也並不可能，因為可能的畫面狀態太龐大。

後來我才注意到我忽略了 Sutton & Barto 一書的設計是先從表格型（tabular methods）方法出發，之後才介紹狀態數量過大而必須以近似函數模擬的案例。因此一開始應該以類似網格遊戲這種可以窮舉狀態和知道環境動態函數當例子會比較自然。

8. 貝爾曼最優方程 #

獎勵是目標的訊號，回報是代理人的目標，價值函數提供了個別狀態或是在個別狀態下採取特定行動時預期得到的回報。作為一種深思熟慮的對未來的計算，價值函數將長期的不確定性資訊用期望值收斂到眼前單一的數字，為代理人的行動提供了完美的指引。

當一個策略 $\pi$ 的價值函數 $v_\pi(s)$ 在所有的狀態下都勝過或等於另外一個策略 $\pi^\prime$ 的價值函數時，我們說 $\pi \ge \pi^\prime$：策略 $\pi $ 優於策略 $\pi^\prime$。又在無數的可能策略之中，至少會存在一個最優策略 $\pi_\ast$，他所對應到的價值函數 $v_\ast(s)$ 在所有的狀態上都是最佳，同時他的行動價值函數 $q_\ast(s,a)$ 在所有的狀態行動組合上也都是最佳的。 $$ v_\ast(s) = \max_{\pi} v_{\pi}(s) \newline q_\ast(s,a) = \max_{\pi}q_\pi(s,a) $$

當採取最佳策略時，我們可以將貝爾曼方程式中關於行動期望值的部分（$\sum_a \pi(s,a)$）改為選擇最佳行動，得到的結果稱為貝爾曼最優方程式（Bellman Optimality Equation）。

$$ v_\ast(s) = \max_a \sum_{s^\prime,r} p(s^\prime, r|s,a) [r + \gamma v_\ast(s^\prime)] $$

$$ q_\ast(s,a) = \sum_{s^\prime,r} p(s^\prime, r|s,a) [r + \gamma \max_{a^\prime} q_\ast(s^\prime, a^\prime) ] $$

價值迭代：解最優策略 #

透過使用貝爾曼最優方程進行迭代策略評估，我們可以計算最優策略 $\pi_\ast$ 下的狀態價值函數 $v_\ast(s)$，這稱為「價值迭代」 value iteration

$$ v_{k+1}(s) = \max_a \sum_{s^\prime,r} p(s^\prime, r|s,a) [r + \gamma v_k(s^\prime)] $$

待方法收練得到最優價值函數後，就可以進一步從中提取出最佳策略：

$$ \pi_\ast(a|s) = \argmax_{a} \sum_{s^\prime,r} p(s^\prime, r|s,a) [r + \gamma v_\ast (s^\prime) ] $$

策略迭代：解最優策略 #

另一種計算最優策略的方法是交替進行「策略評估」和「策略改善」兩種步驟直到收斂，稱為「策略迭代」 policy iteration 。

$$ \pi_0 \xrightarrow{\text E} v_{\pi_{0}} \xrightarrow{\text I} \pi_1 \xrightarrow{\text E} v_{\pi_{1}} \xrightarrow{\text I} \pi_1 \xrightarrow{\text E} v_{\pi_{2}} \xrightarrow{\text I} ... $$

策略評估 policy evaluation（$\xrightarrow{\text E}$）：固定策略 $\pi_k$，計算出符合當下策略的狀態價值 $v_{\pi_{k}}$，policy evaluation 也被稱為預測（prediction）
可以套用前面介紹過的迭代策略評估方法，在固定 $\pi_k$ 的情況下，迭代 $l=0,1,2,...$ 使 $v_l$ 最終收斂到 $v_{\pi_k} $： $$ v_{l+1} = \sum_{a} \pi_{k}(a|s) \sum_{s^\prime,r} p(s^\prime, r | s, a)[r + \gamma v_l(s^\prime)] $$ （這裡改用 $l$ 代表此階段內的迭代過程，避免和 $k$ 混淆。）
策略改善 policy improvement（$\xrightarrow{\text I}$）：固定當下狀態價值函數 $v_{\pi_{k}}$，計算出對應的最佳策略做為新策略
策略改善的做法則是「總是選取當下能帶來最高行動價值的那個行動」，也就是貪婪的概念（greedy）： $$ \pi_{k+1}(s) = \argmax_a \sum_{s^\prime,r} p(s^\prime,r|s,a) [r+\gamma v_{\pi_{k}}(s^\prime) ] $$

當策略迭代方法收斂時 $v$ 和 $\pi$ 不再隨著計算而改變，此時策略和其對應的狀態價值函數達到一致，並且策略就是貪婪的選擇最大價值的行動（否則策略評估步驟會改變 $v$ 或者策略改善步驟會改變 $\pi$），因此最終的 $v$ 和 $\pi$ 就滿足了貝爾曼最優方程式 $$ v_\ast(s) = \max_a \sum_{s^\prime,r} p(s^\prime, r|s,a) [r + \gamma v_\ast(s^\prime)] $$

廣義的策略迭代 #

如果將「策略評估」和「策略改善」廣義的視為兩種階段（而非策略迭代法中精確的步驟），則構成了「廣義策略迭代」generalized policy iteration （GPI）的概念

$$ \text{Policy Evaluation} \rightleftarrows \text{Policy Improvement} $$

GPI 可以幫助我們思考不同強化式學習方法的框架，例如價值迭代法就可以理解為一種廣義策略迭代，和前述策略迭代的差異在於其策略評估階段只迭代更新一次而不是跑到收斂為止。 $$ v_{k+1}(s) = \max_a \sum_{s^\prime,r} p(s^\prime, r|s,a) [r + \gamma v_k(s^\prime)] $$ 上式中的 $\max_a$ 對應到策略改進步驟：將策略設定為貪婪的選取當下最佳價值；而策略評估步驟就是 $v_{k} \rightarrow v_{k+1}$ 的更新，因此價值迭代方法裡每更新一次價值函數（迭代一次而不是跑到收斂），就會更新一次策略。

最優解的裡想 #

目前為止的方法讓我們可以利用價值函數和貝爾曼方程式計算最優策略，可惜這些方法在實際問題上的可行性通常有限。

第一個限制就在於我們必須知道環境的動態函數才能進行價值的計算，這類型的方法也被稱為 model-based 方法，因為需要有一個對世界運作機制精確的知識與描述的 world model。

第二個限制在於所需要的計算資源。價值迭代方法需要對「所有的狀態」進行多輪的計算及更新，因此在狀態數量大的問題上所需的時間和記憶體資源也將變得很巨大。

雖然最優解在我們真正感興趣的強化式學好問題上通常是無法達到的理想，但只要利用實際互動經驗替代無法取得的環境動態函數，就能夠以近似的方式來近似的解貝爾曼最優方程。

9. 蒙地卡羅方法 #

在沒有環境動態函數的情況下我們無法直接進行狀態函數期望值相關的計算，但我們可以透過重複實驗並統計結果的方式模擬環境動態函數的效果，這就是蒙地卡羅方法的精神：以隨機實驗結果的樣本發生頻率來估計事件發生的機率。

如果你想知道擲硬幣時正反面發生機率是否真的相同，透過不斷實驗、紀錄並統計最終正面和反面各自的發生次數，我們就可以逼近兩者發生的機率。每一次的隨機實驗都像是對機率函數的一次抽樣，隨著實驗次數的增加，平均結果也會越來越接近理論上的期望值。

狀態價值函數的估計 #

在有明確終止條件的環境類型中，我們可以利用蒙地卡羅法來估計給定策略的價值函數 $v_\pi(s)$。每一次遵循策略 $\pi$ 並完成一輪完整的互動（episode），就如同進行了一次隨機實驗的採樣。我們紀錄互動歷程中遭遇之狀態及得到的獎勵的軌跡 $s,a,r,...$，就可以在終局時回頭還原每一個狀態 $s_t$ 下最終得到的累積折扣獎勵，並當成一組「狀態＋回報」的配對資料加入我們的統計中。最後再將同一個狀態下所有的回報數據取平均，就得到了狀態價值的估計。

行動價值函數的估計 #

同樣的方法也可以用於估計行動價值函數 $q_\pi(s,a)$。我們可以直接使用隨機實驗的統計數據來評估每次遇到狀態 $s$ 且採取行動 $a$ 然後接下來都遵守策略 $\pi$ 時會得到的平均回報會是多少。行動價值的一個好處是可以直接的轉化爲行動策略，只要貪婪的選擇最高價值的行動即可，不像價值函數還需要配合獎勵函數才能估計下一步的回報來作為選擇行動的依據。

蒙地卡羅方法的特性 #

透過蒙地卡羅方法來估計每個狀態回報的方式和動態規劃的完整計算有幾點不同。

首先是蒙地卡羅中對每個狀態的價值估計是獨立的，只要我們有足夠從該狀態起始的實驗數據，就能夠對該狀態有正確的評估。相對的在動態規劃方法中價值函數的估計公式使用到其他狀態的價值函數。

蒙地卡羅使用隨機實驗的樣本來做價值函數的估計，而樣本的分布會自然傾向發生機率高的事件。因此即使在狀態空間非常大的狀態下，我們仍可以很快的掌握主要的情況而不需要大量但鮮少出現的狀態所造成的龐大計算量所拖累。

探索問題 #

從樣本中學習的方法也帶來了探索問題，如果我們實驗樣本從未探索過某一種可能，那我們就完全沒有關於該狀態的資訊，這可能導致我們錯失更加的選擇。

例如，假設在行動價值的蒙地卡羅估計中我們的實驗遵守的策略導致導致在狀態 $s$ 下我們總是選擇行動 $a$，就會導致 $(s, b)$ 或其他配對從未被選擇過，我們可能因此永遠找不到最佳的策略。要避免這種狀況我們需要確保探索的涵蓋性，理想上我們希望讓實驗的初始狀態 $(s, a)$ 涵蓋所有可能的狀態行動組合，這個概念稱為探索性起始（Exploration starts）。

實際上的做法則可能是讓策略在一開此帶有較高的隨機性以在訓練前期盡可能探索不同的組合，例如常見的 $\epsilon$-greedy 策略會上代理人有 $\epsilon \in [0,1]$ 的機率進隨機選擇行動而不是總是採取當下最高價值的選項。

10. 時序差分學習 #

強化式學習的目標是找尋能最大化累積折扣獎勵的策略，目前為止我們已經有了一套參考方法。

透過價值函數的定義，問題轉化為如何找到最優的價值函數（包含狀態價值函數或者是動作價值函數），而最優策略就是貪婪的選擇最高價值的下一步。
可以用廣義策略迭代來計算最優策略，其做法是反覆兩種步驟的交替迭代
- 第一是策略評估，讓價值函數和當下的策略一致
- 第二是策略改善，用符合當下價值函數的貪婪策略作為新策略。

價值函數的更新目標 #

不同強化式學習方法間主要的差異通常在於進行策略評估的方法，也就是如何估計價值函數。以下三種價值函數的表達形式由上而下分別提示了蒙地卡羅、時序差分（Temporal-Difference TD）、以及動態規劃三種方法各自的更新目標。 $$ \begin{array}{lll} v_\pi(s) & = & \mathbb{E}_\pi [G_{t} | S_t=s] \newline &=& \mathbb{E}_\pi [R_{t+1} + \gamma G_{t+1} | S_t=s] \newline &=& \mathbb{E}_\pi [R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t=s] \end{array} $$

我們用 $s \mapsto u$ 的形式表示狀態 $s$ 的價值估計被朝向目標 $u$ 更新，則動態規劃方法的機制可表達為 $s \mapsto \mathbb{E}_\pi [R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t=s] $：對於狀態 $s$ 我們計算當下狀態價值的期望值來更新其估計。由於每個狀態的更新使用到其他後續遭遇狀態價值的估計值，故具有自舉（自助法 bootstrapping）的性質。又因為需要計算回報的期望值來更新（稱為 expected updates），因此需要環境動態函數。

蒙地卡羅方法則是拿隨機實驗中遭遇的狀態所發生的實際回報來更新其狀態價值 $S_t\mapsto G_t$。因為是使互動實驗中得到的實際回報樣本做更新（稱為 sample update）而不計算期望值，因此不依賴關於環境動態函數的知識。又更新公式中沒有使用到其他狀態的價值估計，因此個別狀態價值估計的更新是獨立、非自舉的（non-bootstrapping）。

TD 方法 #

時序差分學習的更新機制可表達為 $S_t \mapsto R_{t+1} + \gamma v_\pi(S_{t+1})$，是一種結合了兩者特性的方法。他和蒙地卡羅一樣採用 sample update 拿實際互動的樣本經驗更新實際遭遇到的狀態的估計，因此沒有 DP 依賴環境動態函數計算期望值的問題，但他和動態規劃一樣會使用到其他狀態的估計值（bootstrapping），故不會像 MC 方法一樣必須等待回合最終的回報。

考慮到強化式學習的情境以及可能面對非穩定（non-stationary）環境（環境動態函數可能隨時間改變，因此價值函數也可能改變），更新規則也適合以增量式學習（incremental learning 或 online learning 線上學習）的形式：$\text{New} \leftarrow \text{Old} + \alpha [\text{Target} - \text{Old} ]$ 來表達，其中 $\alpha$ 是個參數，代表學習率（learning rate）或更新步伐（step size）。

如此一來一樣都是用實驗樣本做更新的 DP 和 TD 方法可以分別改寫為 $$ V(S_t) \leftarrow V(S_t) + \alpha [G_{t} - V(S_t)] $$ 和 $$ V(S_t) \leftarrow V(S_t) + \alpha [R_{t+1} + \gamma V(S_{t+1}) - V(S_t)] $$

學習目標分別為 $G_{t}$ 和 $R_{t+1} + \gamma V(S_{t+1})$。同時可以定義 TD Error 為 $ \delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) $。

註：本文的 TD 指的是 Sutton & Barto 裡的 TD(0)。

以 TD 學習行動價值 #

如果我們關注的是控制問題（control problem），學習行動價值函數是更直接的選項。行動價值的定義為 $ q_\pi(s,a) = \mathbb{E}_\pi [ R_{t+1}+\gamma G_{t+1}|S_t=s, A_t=a] $，其策略評估的目標的形式和價值函數是相同的。但是為了讓實驗能夠探索涵蓋所有的 $(s,a)$ 組合，要採取例如 $\epsilon$-greedy 方式的策略。

同策略與離策略 #

以樣本學習的方法會衍伸出數據來源為**同策略（on-policy）還是離策略（或異策略 off-policy）**的差異。我們將當下被訓練更新的策略稱為目標策略（target policy），用來跟環境互動產出訓練數據的稱為行為策略（behavior policy）。在同策略方法中我們用同一個策略去產生數據並用來改善自己，也就是目標策略和行動策略是同一個。離策略方法則不限制使用的數據必須由當下策略所產生，可以使用其他行為策略產出數據來訓練目標策略。異策略方法具有更大的彈性，但也帶來訓練不穩定性的挑戰。

Sarsa #

在同策略 on-policy 學習的情況下，因為行動的選擇（$A_t$ 和$A_{t+1}$）都是根據當下的策略，在策略評估時我們可以直接採用以下的更新規則

$$ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t, A_t)] $$

這種方法稱為 Sarsa。

要注意的是 Sarsa 學習到的會是當下策略策略的價值，如果為了保持探索而使用了 $\epsilon$-greedy 策略，就需要讓 $\epsilon$ 在長期下降到零才會趨近於我們真正有興趣的最優策略價值。

Q-Learning #

在異策略 off-policy 學習的情況下，因為訓練樣本數據的來源並非是當下的策略（例如可能是來自探索策略），故我們需要以明確的以最佳策略選則動作–也就是的完全貪婪的選擇下一步 $\max_a$ –而非直接採用實驗數據理的行動所導致的結果，才是我們正確的計算目標。更新規則如下 $$ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma \max_a Q(S_{t+1},a) - Q(S_t, A_t)] $$ 這種方法稱為 Q-learning，對比於 Sarsa，O-learning 學習的目標直接是最佳策略 $\pi_\ast$。

11. 近似解法 #

狀態空間的挑戰 #

目前為止關於最優策略的解法的討論都屬於表格型方法（tabular methods）的範疇，必須要我們的計算資源至少足以維持關於所有狀態的紀錄資訊，才有可能進行計算。然而許多現實問題所面對的狀態空間卻可能是是近乎無窮的。

以圍棋來說，在不考慮規則的情況下其可能狀態共有 $3^{19\times19}\approx 1.74\times10^{172} $ 種（$19\times19$ 個位置，每個位置有無子、黑、白三種可能）。假設以 double precision 也就是 8 byte 來存每個狀態的價值，就會需要約 $10^{164}$ GB 的空間，因此用表格型方法來處理這樣的問題明顯是不可能的。除了儲存空間之外，巨大的狀態空間還會面臨採樣不足和泛化的問題，我們將沒有辦法訪問、涵蓋所有可能的情況，而面對一個從來沒有看過的狀態，表格型方法並無法有效的泛化，也就只能空白以對。

函數近似 #

這樣的情境似乎似曾相識，正是監督式學習方法擅長的領域。如果我們改用參數化的摸型來近似無法以表格完整紀錄的狀態價值函數，就可以將互動取得資料樣本視為訓練資料，監督式機器學習讓我們從有限的輸入輸出案例進行學習，得到具有泛化能力的模型。

具體來說，我們可以用 $\hat{v}(s,\mathbf{w})$ 來近似 $v_\pi(s)$，其中 $\mathbf{w}$ 代表模型的參數，其數量可以遠低於狀態的數量，因此用有限的計算資源就可以處理。如同監督式學習方法一樣，$\hat{v}$ 可以是包含線性方程式、決策樹或是類神經網路等等不同形式的函數。

在參數化模型的情境下，時序差分學習的更新機制可表達為 $S_t \mapsto R_{t+1} + \gamma \hat{v}_(S_{t+1}, \mathbf{w}_t)$，其中價值的計算由參數化模型 $\hat{v}$ 負責，而我們學習的目標也變成如何更新模型參數 $\mathbf{w}$ 來最佳化價值函數的估計模型 $\hat{v}$。隨機梯度下降法（stochastic gradient descent SGD）是最常用的最佳化方法之一，尤其是在採用類神經網路作為模型時。

我們定義價值函數的均方差作為誤差函數為 $$ \overline{\text{VE}}(\mathbf{w}) = \sum_{s\in\cal{S}} \mu(s) [ v_\pi(s) - \hat{v}(s,\mathbf{w}) ]^2 $$ 其中 $\mu(s)$ 是一個總和為一的權重函數，表達我們如何衡量不同狀態的貢獻（畢竟每個狀態出現的頻率可能差別很大）。$\overline{\text{VE}}$ 衡量了狀態價值估計與真實值之間的誤差，被用於評估近似函數的表現並指引學習的方向。

假設我們從實驗中取得的樣本數據包含了隨機狀態 $S_t$ 和其真正的價值 $v_\pi(S_t)$（也就是精確的目標值），並且定義 $\mu$ 為採樣時狀態樣本出現的頻率（意思是我們限制計算的範圍在實際出現的樣本內，不管其他的狀態），則 $\overline{\text{VE}}$ 回歸到樣本的 mean square error。在 SGD 方法中我們以計算損失函數對模型參數的微分，並據以調整參數使誤差降低。

$$ \begin{array}{lll} \mathbf{w}_{t+1} & = & \mathbf{w}_{t} - \frac{1}{2}\alpha \nabla [v_\pi(S_t) - \hat{v}(S_t,\mathbf{w}_t)]^2 \newline & = & \mathbf{w}_t + \alpha[v_\pi(S_t) - \hat{v}(S_t,\mathbf{w}_t)] \nabla \hat{v}(S_t,\mathbf{w}_t) \end{array} $$

半梯度方法 #

在現實上我們通常不會拿到狀態 $S_t$ 和其精確的目標答案 $v_\pi(S_t)$，而會是某種估計 $U_t$，一般性的 SGD 公式可寫為 $$ \mathbf{w}_{t+1} = \mathbf{w}_t + \alpha[U_t - \hat{v}(S_t,\mathbf{w}_t)] \nabla \hat{v}(S_t,\mathbf{w}_t) $$

當 $U_t$ 是真正價值的不偏估計 $\mathbb{E}[U_t|S_t] = v_\pi(s) $，則此更新仍可以保證收斂到局部最佳。但在自舉法的情況下由於所有目標的計算都是基於當下的模型參數 $\mathbf{w}_t$，並不是真正目標的不偏估計，就不具有相同的保證。

如果 $U_t$ 本身是基於 $\hat{v}$ 所得到，例如 TD 的目標是 $ U_t = R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}) $，那麼在前述 SGD 的 $\mathbf{w}$ 更新公式裡我們實際上是忽略掉了目標部分的梯度分支 $\nabla U_t$，因此這種方法也被稱為半梯度下降，而其對應的 TD 方法就是 semi-gradient TD。

致命三元組 #

書中將以下三個要素稱為致命三元組（Deadly Triad），當三種情況並存時，訓練不保證收斂並可能面臨不穩定和高變異的情況

函數近似（Functional approximation）
自舉法（Bootstrapping）
離策略訓練（Off-policy training）

書中詳細的討論我只有大致的瀏覽，不過應可以比較直覺的理解為三者各自帶有的誤差可能會彼此加強並且反覆傳播，導致不穩定甚至發散。

函數近似和自舉法背後都涉及了估計值之間的交互作用：使用函數近似時更新一個狀態的權重時也會連帶影響到其他狀態的估計值，而自舉法則是使用其他狀態的估計值來更新自己的狀態的估計，兩者結合起來可能會發生當下狀態估計值的上升導致其他狀態的估計上升，然後其他上升的狀態值又被用於自己狀態的估計而導致自己的上升如此的迴圈，因自我增強的回饋導致估計的發散。

離策略訓練的誤差則來自行為測略所採樣到的數據分布和目標策略不同，目標策略所選擇到行動和接續狀態不一定被行為策略採樣涵蓋到，因此其價值估計可能持續保持在不正確的估計數值上而不被更新。相對的同策略的方法則會持續在相關的後續狀態和行動範圍內採樣並完善其正確的價值估計。

不穩定性的問題在致命三元組中只有兩者存在時可以被避免，由於採用函數近似在處理大狀態空間的問題時是必要的，可能的權衡通常來自自舉法和離策略訓練。

12. Deep Q-Network #

Deep Q-Network 由Ｍnih et al. 在 2013 年首次提出，以類神經網路為行動函數的近似模型，搭配經驗回放的設計並使用半梯度下降的 Q-learning 加上 $\epsilon$-greedy 策略來讓代理人學習玩 Atari 遊戲，以下為模型權重的更新公式

$$ \mathbf{w}_{t+1} = \mathbf{w}_t + \alpha[ R_{t+1} + \gamma \max_a \hat{q}(S_{t+1}, a, \mathbf{w}_t) - \hat{q}(S_t,A_t,\mathbf{w}_t)] \nabla \hat{q}(S_t,A_t,\mathbf{w}_t) $$

利用前面從 MDP 出發所建立起的基礎，我們現在可以嘗試往回追溯這一條公式的脈絡：

由於 Atari 遊戲可能的狀態空間（可能出現的遊戲畫面組合）太大無法以表格型方法處理，故以類神經網路模型 $\hat{q}$ 作為行動價值 $q$ 的參數化模型。
行動價值函數本質上是採取行動時對未來累積折扣獎勵（回報）的期望值，正確的行動價值估計可以直接轉化最優策略，也就可以最大化代理人的目標。我們需要透過學習調整模型參數 $\mathbf{w}$ 出好的近似函數 $\hat{q}$。
此更新形式的背後的概念是應用 TD 學習的 Q-learning，來自於貝爾曼方程式的遞迴表式。Q-learning 是 off-policy 方法，也是公式中用 $\max_a$ 採用貪婪策略的原因。
TD 學習和 MC 方法一樣是樣本更新，以互動歷程元組 $(s_t, a_t, r_{t+1}, s_{t+1}) $ 經驗構成訓練資料。相較之下 DP 的期望更新計算需要環境動態的知識，這裡並不需要。
訓練方法是半梯度的 Q-learning，以 $R_{t+1} + \gamma \max_a \hat{q}(S_{t+1}, a, \mathbf{w}_t) $ 的值為目標，目標本身雖然也依賴於 $\mathbf{w}$ ，但並不考慮其梯度。
行動價值和互動歷程背後的數學模型是 MDP，MDP 的五元組為 $\langle \cal{S}, \cal{A}, \mathit{T}, r, \gamma \rangle $

改善不穩定性 #

經驗回放方法在 DQN 的穩定訓練中扮演了重要的角色，具體來說我們將代理人與環境互動一步的轉移（transition）結果以元組 $(S_t, A_t, R_{t+1},S_{t+1})$ 的方式儲存下來作為經驗，在梯度下降的 mini-batch 抽樣時隨機取出作為訓練資料使用。由於 Q-learning 屬於離策略的學習方法，因此本就可以使用其他經驗，又相較於標準的 Q-learning 方法可能使用連續的互動資料做訓練，經驗回放的隨機抽養打斷了訓練資料前後的關聯性，降低了不穩定性。

另一個改善穩定性的方法是將選擇策略的網路和被訓練（被更新權重的網路）分離，做法是將目標網路 $\hat{q}$ 的權重複製到另外一個網路 $\tilde{q}$ 中，並由 $\tilde{q}$ 負責選取行動。由於 $\tilde{q}$ 大部分時候是固定不變，每過一段時間才會更新一次跟上 $\tilde{q}$ 的最新權重，如此可以讓以下新的更新公式中作為目標值一部分的 $\max_a \tilde{q}(S_{t+1},a,\mathbf{w}_t) $ 不再那摩直接的依賴於被訓練模型的參數，更接近監督式學習的做法中的穩定目標值。

$$ \mathbf{w}_{t+1} = \mathbf{w}_t + \alpha[ R_{t+1} + \gamma \max_a \tilde{q}(S_{t+1}, a, \mathbf{w}_t) - \hat{q}(S_t,A_t,\mathbf{w}_t)] \nabla \hat{q}(S_t,A_t,\mathbf{w}_t) $$

註：我的理解如果正確的話 $\tilde{q} $ 的權重 $\mathbf{w}_t$ （大部分時間）應該是被固定在另一個較早時間的版本，因此上式中 $\tilde{q} $ 裡的 $\mathbf{w}_t$ 也許應該用其他的符號來表達才不會跟 $\hat{q} $ 的參數混淆？

後記 #

Sutton & Barto 一書的內容既廣且深，不只介紹個別方法，更嘗試將各種模型和訓練方法的差異放在統一的脈絡框架下說明，可以感受到大師的高度和視野。

不過也因為其豐富的內容，開始閱讀後我決定將主要目標設定在嘗試串連 MDP 到 DQN 之間的基礎觀念就好，對於沒那麼直接相關的深入討論或是範例就先略讀或跳過以免欲罷不能，即便如此也已經是收穫良多。其他還有好些想了解的主題像是 Policy Gradient、Planning、Alpha Go/Alpha Zero、以及第三部分和心理學及神經科學的討論，只能留待將來了。

從 AI 發展的角度來看，大概沒有人能預測強化式學習本身有沒有機會像 LLM 一樣經歷某種突破或是爆發。我個人是覺得不論如何，這個領域有著一般化的框架、豐富的觀念和研究素材、方法的設計，將來應該會持續為機器學習領域提供探索與思考的方向。如果哪一天有辦法在強化式學習「環境」的取得和利用面上有什麼重大突破（如同 LLM 成功利用了人類龐大的數位文本），也許就能打開意想不到的篇章。